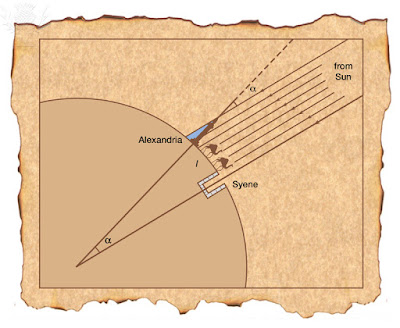
Eratosthenes's Earth

Eratosthenes' measurement of the Earth. Illustration. Britannica ImageQuest, Encyclopædia Britannica

Thousands of years before Columbus headed west from the Canary Islands in search of new lands, Eratosthenes used the Egyptian landscape and the sun to calculate the circumference of the earth. He was the head librarian of the famous library of Alexandria in the third century BCE.

A friend of his lived in the town of Aswan (then called Syene) in upper Egypt. This friend mentioned that at noon on the summer solstice, the sun cast no shadow at all; in fact the sun would even illuminate the water in a very deep well. Intrigued by this fact, Eratosthenes went out at noon on the summer solstice and saw that in Alexandria the sun did cast a shadow and the rays hit the earth at an angle of 7.2 degrees. Of course, he did not have our modern units of degrees and instead measured this angle as \(\frac{1}{50}\) of a circle. Now instead of just noting this fun fact, Eratosthenes realized that he could use it to calculate the circumference of the earth.

For the method to work, Eratosthenes needed to make two assumptions which, fortunately, we now know are valid.

1. The earth is round. It should be clear that the question of the circumference of the earth does not even make sense if this is not true.
2. The sun is so large and far away that its rays are parallel to each other as they hit the earth. 

These two assumptions together mean that the curvature of the earth is responsible for the difference in the angle the sun’s rays hit the earth in Aswan and in Alexandria as seen in the diagram above.

Notice that the angle the sun makes in Alexandria is the same as the angle from the center of the earth, which is \(\frac{1}{50}\) of a circle. Therefore the arc between Aswan and Alexandria must be \(\frac{1}{50}\) of the circumference of the earth. In other words, the circumference of the earth is 50 times the distance from Aswan to Alexandria. This distance is 843km so the earth must have a circumference of 42,150 km. The actual circumference of the earth is estimated to be 40,075 which tells us that our answer is within 6% of the correct one.

As with the units for the angle, Eratosthenes did not use kilometers for this measurement. Instead he used stadia. The conversion between kilometers and stadia is unknown as it did not have a consistent definition in antiquity. Therefore, there is dispute about how accurate Eratosthenes’s result was. 

However, we can work backwards from Eratosthenes’s result of 252,000 stadia to obtain a conversion factor. The distance between Alexandria and Aswan must have been measured as 5040 stadia since it is \(\frac{1}{50}\) of the circumference of the earth. It is unlikely that his measurement for this distance was as precise as our current measurement of 843km but equating 5040 stadia with 843km gives us a conversion of \(\frac{843,000m}{5040s}\approx 167\) meters per stadion. This is well within the  accepted range of 157-209 meters and is evidence that his estimate for the circumference of the world was quite good.

Some questions for future explorations:

• Can you use or adapt this method if the sun is not directly overhead in either town?
• Does longitude or latitude affect the measurements?
• Do the measurements need to be taken at the solstice? In other words, does the tilt of the earth affect the results?
• How would you adapt this method to estimate the radius of the earth?

Further reading:

• E Gulbekian, The origin and value of the stadion unit used by Eratosthenes in the third century B.C, Arch. Hist. Exact Sci. 37 (4) (1987), 359-363.
• Rawlins, Dennis, The Eratosthenes-Strabo Nile Map. Is It the Earliest Surviving Instance of Spherical Cartography? Did It Supply the 5000 Stades Arc for Eratosthenes' Experiment?. Arch. Hist. Exact Sci. 26 (3) (1982), 211-219.